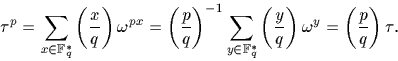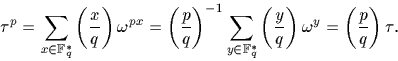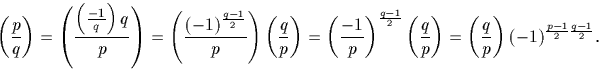Next: Extraction de racine carrée
Up: Quod erat demanstrandum (bis
Previous: Lemme sur la somme
La somme de Gauss 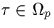 est une racine carrée de
est une racine carrée de 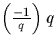 ;
il s'ensuit que
;
il s'ensuit que 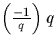 est un
carré dans
est un
carré dans 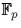 si et seulement si
si et seulement si 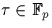 . Rappelons à cette
occasion qu'un élément
. Rappelons à cette
occasion qu'un élément 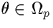 appartient à
appartient à
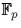 si et seulement si
si et seulement si 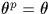 : en effet, le polynôme Xp-X a
au plus p racines dans le corps
: en effet, le polynôme Xp-X a
au plus p racines dans le corps 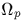 et
tous les éléments de
et
tous les éléments de 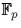 sont racines. Le calcul de
sont racines. Le calcul de 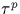 est
facilité par le fait que nous sommes en caractéristique p :
est
facilité par le fait que nous sommes en caractéristique p :
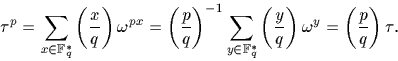
On en déduit que 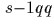 est un carré dans
est un carré dans 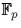 si et seulement si
p est un carré modulo q.
Il vient donc :
si et seulement si
p est un carré modulo q.
Il vient donc :
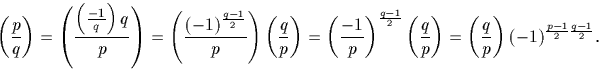
QED.
Cyril Banderier
7/23/1997