



Next: Retour à notre seconde
Up: Quod erat demanstrandum (bis
Previous: Quod erat demanstrandum (bis
Avec les notations précédentes, on a : 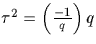 .Preuve :
On a
.Preuve :
On a
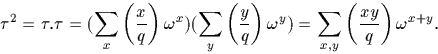
Réalisons le changement de variable y=xz et, en utilisant
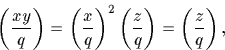
on
a :
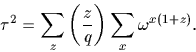
Or
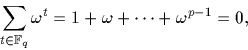
par conséquent
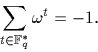
Si 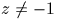 , l'application
, l'application 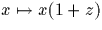 est une permutation de
est une permutation de
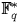 donc
donc
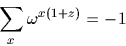
et
donc
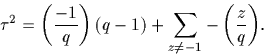
Si on utilise maintenant
le fait qu'il y a dans 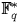 autant de carrés que de non carrés, ce
qui entraîne
autant de carrés que de non carrés, ce
qui entraîne
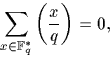
on
obtient ce que l'on voulait :
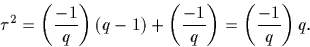
Une généralisation abstraite (le théorème de Kronecker-Weber) affirme
que tout corps de nombres algébriques
dont le groupe de Galois sur 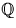 est commutatif est un sous-corps d'un corps
cyclotomique.
est commutatif est un sous-corps d'un corps
cyclotomique.
Cyril Banderier
7/23/1997
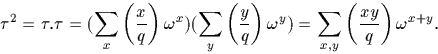
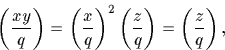
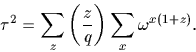
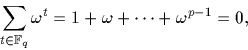
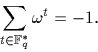
![]()
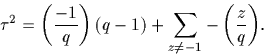
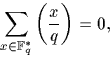
![]()
![]() est commutatif est un sous-corps d'un corps
cyclotomique.
est commutatif est un sous-corps d'un corps
cyclotomique.