



Next: Réciprocité dans un corps
Up: Réciprocité dans un corps
Previous: Fonction de Weierstrass et
Le symbole quadratique 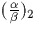 est défini pour
est défini pour ![$\alpha,
\beta \in {\mathbb Z}[i]$](img325.gif) et
et 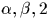 étrangers (ce qui est désormais supposé) par
étrangers (ce qui est désormais supposé) par
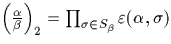 où
où 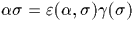 avec
avec 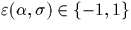 , où
, où
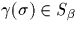 et où
et où 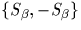 est un système
complet de représentants (
est un système
complet de représentants (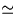 une partition) de
une partition) de 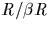 .
.
Cyril Banderier
7/23/1997