



Next: Définition du symbole quadratique
Up: Réciprocité dans un corps
Previous: Une formule accorte
Nous aurons besoin de la fonction 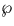 de Weierstrass qui est à la base de
la théorie des courbes elliptiques dont les résultats suivants dérivent
[Bayad], [Lang].
Soit R le réseau
de Weierstrass qui est à la base de
la théorie des courbes elliptiques dont les résultats suivants dérivent
[Bayad], [Lang].
Soit R le réseau 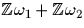 .
.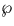 est définie par
est définie par
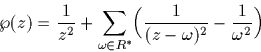
On peut sommer sur R car il y a convergence normale donc commutative.
On note
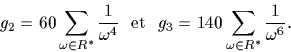
On obtient ainsi la formule clef reliant la fonction de Weierstrass aux courbes
elliptiques, permettant de considérer 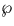 comme une ``paramétrisation''
de la courbe elliptique E :
comme une ``paramétrisation''
de la courbe elliptique E :
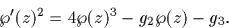
Ainsi (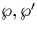 ) paramétrise
Y2=4X3-g2X-g3, de discriminant :
) paramétrise
Y2=4X3-g2X-g3, de discriminant : 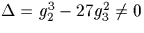 .On a ainsi un isomorphisme entre
.On a ainsi un isomorphisme entre 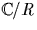 et E donné par
et E donné par
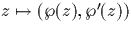 .
.
Cyril Banderier
7/23/1997
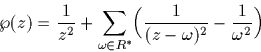
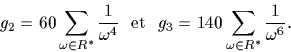
![]()