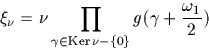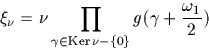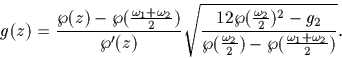Next: Loi de réciprocité quadratique
Up: Réciprocité dans un corps
Previous: Définition du symbole quadratique
Quand le discriminant D est différent de -4,-3, i.e.
quand on est dans 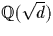 avec d différent de -1, -3,
avec d différent de -1, -3,
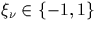 est défini par
est défini par
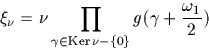
où g est la fonction elliptique associée au réseau R définie par
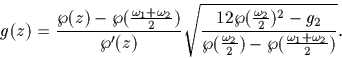
Rappelons que 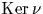 désigne le noyau de la multiplication
par
désigne le noyau de la multiplication
par 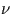 , i.e. le noyau de l'endomorphisme de E qui à
, i.e. le noyau de l'endomorphisme de E qui à 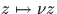 .
.
Cyril Banderier
7/23/1997