



Next: Le symbole de Jacobi
Up: Épisode second : un peu
Previous: Épisode second : un peu
On définit 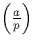 pour p premier comme égal à 1 si a est un
carré dans
pour p premier comme égal à 1 si a est un
carré dans 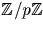 , à -1 sinon.
Ce symbole est multiplicatif :
, à -1 sinon.
Ce symbole est multiplicatif :
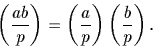
Ceci est dû au fait que le produit de deux carrés est un carré,
(ceci est toujours vrai dans un groupe cyclique 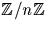 ) et que, si nous
sommes dans
) et que, si nous
sommes dans 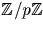 , p premier,
alors le produit d'un carré par un non carré est un non carré et le
produit de deux non carrés est un carré.
, p premier,
alors le produit d'un carré par un non carré est un non carré et le
produit de deux non carrés est un carré.
On peut aussi énoncer le fait suivant :
g est un générateur du groupe
cyclique  est un non carré.
La réciproque est vraie si
est un non carré.
La réciproque est vraie si 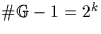 .
.
La loi de réciprocité pour le symbole de Legendre affirme
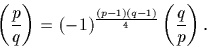
Ainsi, de même que dans l'algorithme d'Euclide pour le calcul du PGCD ou que
dans le test de primalité par descente-remontée (voir §),
on est ramené, de proche en proche, à traiter des nombres de plus en plus
petits.
L'intérêt d'une stratégie de ``rapetissement progressif du
problème'' transparaît dans l'algorithme de calcul du pgcd de
(a,b)= :(r,s), dont voici l'algorithme :
DEBUT
tant que 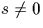 faire
faire 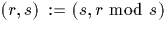 ;
;
(* on crunche et squeeze avec allégresse *)
retourner r ;
FIN




Next: Le symbole de Jacobi
Up: Épisode second : un peu
Previous: Épisode second : un peu
Cyril Banderier
7/23/1997
![]()
![]() est un non carré.
La réciproque est vraie si
est un non carré.
La réciproque est vraie si ![]() .
.![]()
![]() faire
faire ![]() ;
;