Next: Loi de réciprocité quartique,
Up: Pour quelques réciprocités de
Previous: Pour quelques réciprocités de
Les nombres p-adiques ont été introduits par Hensel, on peut se les
représenter
comme l'ensemble des nombres 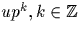 et u inversible.
Le symbole de Hilbert sur les nombres p-adiques est défini comme suit :
et u inversible.
Le symbole de Hilbert sur les nombres p-adiques est défini comme suit :
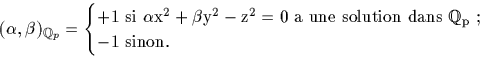
On a le résultat suivant : α est un carré si 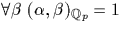 .
.
Auteur : Cyril Banderier, 23 juillet 1997.