



Next: Loi de réciprocité pour
Up: Réciprocité et nombres premiers
Previous: Nombres premiers réguliers
On peut considérer la conjecture de Fermat comme un baromètre de
l'évolution de la théorie des nombres et de l'algèbre. Il en est
de même des lois de réciprocité. Il serait sans doute excessif d'affirmer
que, sans ces deux problèmes, les mathématiciens
n'auraient pas développé les notions de congruence, d'idéal, d'analyse
complexe (via le théorème des nombres premiers [voir
§] et via le théorème de la progression arithmétique
[voir §]), de corps de classes (et donc les idèles de
Chevalley puis les adèles de Weil), de courbes elliptiques...En revanche,
on affirmera sans vergogne le rôle moteur de ces deux problèmes.
Il est toutefois amusant de remarquer que la victoire sur le théorème de
Fermat ne s'est pas faite avec la théorie développée
par Kummer : en fait la méthode de Wiles, qui permet de montrer
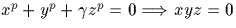 pour
pour 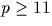 et γ
puissance d'un nombre premier impair, est basée sur les courbes elliptiques,
nouvelle drogue des mathématiciens, pour
ceux qui voudraient s'y mithridatiser confer [Hellegouarch] et [Lang].
et γ
puissance d'un nombre premier impair, est basée sur les courbes elliptiques,
nouvelle drogue des mathématiciens, pour
ceux qui voudraient s'y mithridatiser confer [Hellegouarch] et [Lang].
Cyril Banderier
7/23/1997