



Next: Réciprocité et tests de
Up: Extraction de racine carrée
Previous: Méthode de Shanks
Nous allons calculer une racine carrée de x0=160 dans 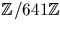 avec la méthode Shanks. On a p=641=5.27+1, i.e. q=5, k=7
et on peut vérifier que
avec la méthode Shanks. On a p=641=5.27+1, i.e. q=5, k=7
et on peut vérifier que 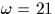 est un générateur de
est un générateur de 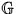 .
.
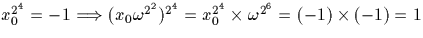
On pose 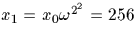 , si bien que x124=1. On vérifie
que x1 est d'ordre 8, d'où :
, si bien que x124=1. On vérifie
que x1 est d'ordre 8, d'où :
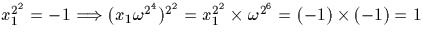
On pose 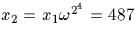 , si bien que x222=1. On vérifie que
x2 est d'ordre 4, d'où :
, si bien que x222=1. On vérifie que
x2 est d'ordre 4, d'où :
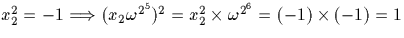
Et on s'arrête car 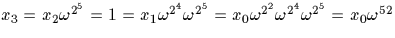 ,si bien que
,si bien que 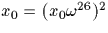 i.e.
i.e. 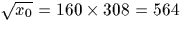 .
.
Cyril Banderier
7/23/1997