



Next: Calcul de
Up: Quelques démonstrations de la
Previous: Calcul de
Il s'agit de calculer 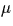 pour m=-3,
i.e. le nombres de résidus minimaux de
pour m=-3,
i.e. le nombres de résidus minimaux de 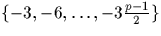 strictement négatifs.
On est donc ramené à compter les entiers k tels que : p/2 <-3k<p.
strictement négatifs.
On est donc ramené à compter les entiers k tels que : p/2 <-3k<p.
- Si
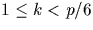 alors
alors 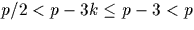 , les résidus minimaux sont
strictement négatifs.
, les résidus minimaux sont
strictement négatifs.
- Si p/6 < k <p/3 alors 0<p-3k<p/2, les résidus minimaux ne sont pas
strictement négatifs, donc on ne retient pas ces valeurs de k.
- Si p/3 < k < p/2 alors p/2<2p-3k < p, les résidus minimaux sont
strictement négatifs.
Ainsi, les valeurs de k pour lesquelles les résidus minimaux sont
strictement négatifs sont : 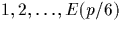 et
et
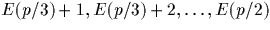 donc
donc 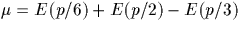 .D'où si p=6n+1 alors
.D'où si p=6n+1 alors 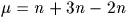 est pair et si p=6n+5
alors
est pair et si p=6n+5
alors 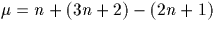 est impair.
est impair.
En résumé :
-3 est un carré modulo 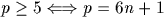 .
.
Cyril Banderier
7/23/1997
![]() .
.