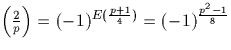 où E(x) désigne la partie entière de x,
i.e. le plus petit entier
où E(x) désigne la partie entière de x,
i.e. le plus petit entier
Il s'agit de calculer ![]() pour m=2, i.e. le nombres de résidus minimaux
de
pour m=2, i.e. le nombres de résidus minimaux
de ![]() strictement négatifs.
strictement négatifs.
On est donc ramené à compter les entiers k tels que : p/2 < 2k<p.
On vérifie aisément que si ![]() et
et
![]() .
.
Si ![]() et
et
![]() .
.
Ainsi, dans tous les cas : ![]() . Notons
. Notons
![]() . Ainsi
. Ainsi ![]() et si
et si
![]() (resp.
(resp. ![]() ), r a
la même parité que
), r a
la même parité que ![]() (resp.
(resp. ![]() ).
Donc, dans tous les cas, r a même parité que
).
Donc, dans tous les cas, r a même parité que ![]() et :
et :
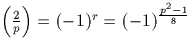 .
.
En résumé :
2 est un carré modulo ![]() .
.