



Next: Critère d'Euler
Up: Quelques démonstrations de la
Previous: Quelques démonstrations de la
Ce paragraphe et les suivants sont directement recopiés sur [Francinou], ces
derniers étant eux-mêmes parfois directement
repiqués sur [Hardy]...Mais puisque ni une démonstration ni une mise en
page ne peut être copyrightée, n'ayons pas d'état d'âme
et saluons ainsi ces deux ouvrages de références, quoiqu'aux ambitions
différentes.
Soit 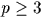 un nombre premier (notation conservée dans TOUT ce chapitre).
un nombre premier (notation conservée dans TOUT ce chapitre).
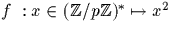 est un endomorphisme du groupe multiplicatif
du corps
est un endomorphisme du groupe multiplicatif
du corps 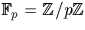 .Son noyau est {-1, +1}, les racines de X2-1. Le noyau étant de cardinal 2,
l'image de f est de cardinal
Card(
.Son noyau est {-1, +1}, les racines de X2-1. Le noyau étant de cardinal 2,
l'image de f est de cardinal
Card(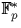 )/Card(
)/Card(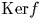 )
)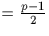 . Il y a donc
. Il y a donc 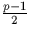 carrés dans
carrés dans 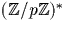 . 0 étant
aussi un carré,
. 0 étant
aussi un carré, 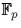 contient
contient 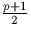 carrés.
carrés.
Cyril Banderier
7/23/1997
![]() un nombre premier (notation conservée dans TOUT ce chapitre).
un nombre premier (notation conservée dans TOUT ce chapitre).
![]() est un endomorphisme du groupe multiplicatif
du corps
est un endomorphisme du groupe multiplicatif
du corps ![]() .Son noyau est {-1, +1}, les racines de X2-1. Le noyau étant de cardinal 2,
l'image de f est de cardinal
Card(
.Son noyau est {-1, +1}, les racines de X2-1. Le noyau étant de cardinal 2,
l'image de f est de cardinal
Card(![]() )/Card(
)/Card(![]() )
)![]() . Il y a donc
. Il y a donc ![]() carrés dans
carrés dans ![]() . 0 étant
aussi un carré,
. 0 étant
aussi un carré, ![]() contient
contient ![]() carrés.
carrés.