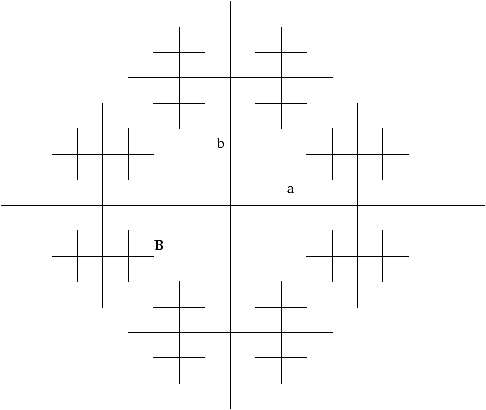The Local Limit Theorem for Random Walks on Free Groups

The Local Limit Theorem for Random Walks on Free Groups

Steve Lalley

Purdue University

Algorithms Seminar

May 31, 1999

[summary by Cyril Banderier]

A properly typeset version of this document is available in postscript and in pdf.

If some fonts do not look right on your screen, this might be fixed by configuring your browser (see the documentation here).

Abstract

Local limit theorems and saddlepoint approximations are given for random walks on a free group whose step distributions have finite support. These are derived by exploiting a set of algebraic relations among certain generating functions that arise naturally in connection with the transition probabilities of the random walks. Basic tools involved in the analysis are the elementary theory of algebraic functions, the Perron-Frobenius theory of nonnegative matrices, and standard techniques of singularity analysis.

1 Walks on Groups

Figure 1: A representation (Cayley graph) of the infinite free group Z * Z

Let G be a the free group with generators a₁,..., a_L. For example, the free group Z * Z has two generators a and b. The word a b a a^_ b^_ a^_ a^_ b^_ a a corresponds to the point B, the associated reduced word is a^_ b^_ a a.

A finite-range random walk {Z_n}_{n³ 0} is a Markov chain on G with Z₀:=e (the identity of the group, the ``origin'', the starting point) and transition probabilities

Pr{Z_n+1=yx|Z_n=y}=p_x " x,y Î G, n³ 0,

where p_x for xÎ G is a probability distribution with finite support (in other words, p_x is the probability of the ``jump'' x).

Note p^*n(x) the probability of being in x after n steps. It is assumed that the random walk is irreducible and aperiodic, that is, that

" x Î G

n³ 1

p^*n(x) >0 (irreducibility);

GCD{n; p^*n(e)>0}=1 (aperiodicity).

Another important condition is the following:

Positivity: p_e>0 and p_g>0 for all generators g of G (and their inverses).

Similarly to the random walk in the Euclidian case Z^d, a local limit theorem is given by the asymptotics

p^*n(x)~

B_x R^-n

(2 p R)^1/2n^3/2

Similar results were already known when all the steps are of size one (nearest neighbour random walk [3]) or when all the words at a same distance from the origin are equiprobable (the so-called isotropic random walk [2, 8, 9]).

2 Singularity Analysis

This section is devoted to the analysis of some probability generating functions (PGF) related to the walk. For xÎ G and zÎ C (|z|<1), define

the random variable coding where one is after n steps: Z_n,
the PGF to reach x in n steps: G_x(z):=å_n p^*n(x)zⁿ,
the PGF of the excursions (Green's function): G(z):=G_e(z),
the first time x is reached: T_x:=inf{n³ 0: Z_n=x},
the PGF to reach x for the first time in n steps: F_x(z):=å_n Pr{T_x=n} zⁿ.

Note that aperiodicity and irreducibility imply that for all sufficiently large n³ 1, p^*n(e)>0 and p^*n(y)>0, for any (inverse of a) generator y.

The following (combinatorially trivial) relations

G_x(z)=F_x(z)G(x),

G(z)=1+z

æ
ç
ç
è

p_e+

x¹ e

p_x F

x^-1

(z)

ö
÷
÷
ø

G(z)=

æ
ç
ç
è

1-zp_e-z

x¹ e

p_x F

x^-1

(z)

ö
÷
÷
ø

-1

allow to prove that all of the functions F_x and G_x have the same radius of convergence R, 1<R<¥ (the less obvious is that R is strictly greater than 1).

Let B be the set of points at distance £ K, where K is such that there is no smaller ball in which the support of the step distribution {p_x} is contained. Define now

the first time that x is exceeded: t_x
the PGF to go from a to xb while x as never been exceeded before:

H_x^ab=

å

n
Pr {Z_n=xb|Z₀=a and Z_i<nÏxB } zⁿ
the PGF to go from x to the origin: F_x^_-1(z)

The formula

" x¹ e F_x(z)=

bÎ B-{e}

H_x^eb (z) F

b^-1

(z)

leads to an expression of F_x=uH_x(z)v=u H_x_₁(z)··· H_x_{_m}(z)v where u is the projection on e and v a vector whose entries are the F_b^_-1(z) for bÎ B and where the product of matrices is over x₁··· x_m, the reduced word associated to x.

It is then proven by the Markov property that all the non-constant H_x_{_i}^ab satisfy polynomial relations (H_x_{_i}=Q_i(H_x_₁, H_x_₂, ...), see [6] for exact relations) and that they have the same radius of convergence.

By elimination (Gröbner basis or resultants), the functions F_x and G_x are algebraic. Their Puiseux expansion leads to an algebraic singularity with exponent 1/2.

Here is a sketch of the proof that the exponent is indeed a=1/2. Define J_z the Jacobian matrix (¶ Q_i / ¶ H_x_{_j}), the polynomials Q_i have nonnegative coefficients, thus there exists n such that J_zⁿ is an aperiodic and irreducible matrix with strictly positive coefficients. By the Perron-Frobenius theorem, J_z has a positive eigenvalue l_z of multiplicity 1. The function l_z is increasing and real-analytic and l_R=1/R. Considering a left eigenvector of J_R and using the shape of the Q_i yields to the relations (R-z)(C+···)=C'(R-z)^2a+···, thus 2a=1.

As z=R is the dominant singularity of F_x and G_x, one has the two following theorems:

Theorem 1 [Local limit theorem, access] Assuming irreducibility and aperiodicity, one has, for a positive constant B_x:

p^*n(x)~

B_x

(2p R)^1/2Rⁿ n^3/2

Theorem 2 [Local limit theorem, first access] Assuming positivity, one has, for a positive constant A_x:

Pr {x is reached for the first time after n steps} ~

A_x

(2p R)^1/2Rⁿ n^3/2

3 Saddlepoint Approximations

The probability to reach a point x at a distance m of the origin in n steps is

p^*n(x)~

exp(nb(m/n))

(

(m/n))^1/2

C(m/n)

for appropriate functions b, C and y^.. (see the correct definitions / notations in [6]).

This uniform asymptotics in x and n corresponds to the classical saddlepoint approximation (sharp large deviations theorems) for sums of iid random vectors in R^d.

The saddlepoint approximations are of interest for another reason. For large n, nearly all the mass in the probability distribution p^*n(x) is concentrated in the region |x|³ e n, where the local limit approximations are not accurate. This contrasts with the situation for finite range random walk in Euclidean space. In fact, Guivarch [4] has shown that for random walks in G, the distance from the origin grows linearly in n. Sawyer and Steger [10] have further shown that (|Z_n|-nb)/(n)^1/2 converges in law to a normal distribution.

Finally, S. Lalley, using a special matrix product and results on Ruelle's Perron-Frobenius operators, derives a saddlepoint approximation, uniformly for m/n in a given compact

Pr{|Z_n|=m}~

exp(nB(m/n))

(2 p m D(m/n))^1/2

C(m/n).

References

[1]: Cartwright (Donald I.) and Sawyer (Stanley). -- The Martin boundary for general isotropic random walks in a tree. Journal of Theoretical Probability, vol. 4, n°1, 1991, pp. 111--136.
[2]: Figà-Talamanca (Alessandro) and Picardello (Massimo A.). -- Harmonic analysis on free groups. -- Marcel Dekker Inc., New York, 1983, viii+145p.
[3]: Gerl (Peter) and Woess (Wolfgang). -- Local limits and harmonic functions for nonisotropic random walks on free groups. Probability Theory and Related Fields, vol. 71, n°3, 1986, pp. 341--355.
[4]: Guivarc'h (Y.). -- Sur la loi des grands nombres et le rayon spectral d'une marche aléatoire. In Conference on Random Walks (Kleebach, 1979), pp. 47--98, 3. -- Société Mathématique de France, Paris, 1980.
[5]: Lalley (Steven P.). -- Saddle-point approximations and space-time Martin boundary for nearest-neighbor random walk on a homogeneous tree. Journal of Theoretical Probability, vol. 4, n°4, 1991, pp. 701--723.
[6]: Lalley (Steven P.). -- Finite range random walk on free groups and homogeneous trees. The Annals of Probability, vol. 21, n°4, 1993, pp. 2087--2130.
[7]: Lalley (Steven P.) and Hueter (Irene). -- Anisotropic branching random walks on homogeneous trees. Preprint, 1999.
[8]: Picardello (Massimo A.). -- Spherical functions and local limit theorems on free groups. Annali di Matematica Pura ed Applicata. Serie Quarta, vol. 133, 1983, pp. 177--191.
[9]: Sawyer (Stanley). -- Isotropic random walks in a tree. Zeitschrift für Wahrscheinlichkeitstheorie und Verwandte Gebiete, vol. 42, n°4, 1978, pp. 279--292.
[10]: Sawyer (Stanley) and Steger (Tim). -- The rate of escape for anisotropic random walks in a tree. Probability Theory and Related Fields, vol. 76, n°2, 1987, pp. 207--230.
[11]: Seneta (E.). -- Nonnegative matrices and Markov chains. -- Springer-Verlag, New York, 1981, second edition, xiii+279p.

This document was translated from L^AT_EX by H^EV^EA.