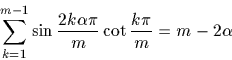Dans la généralisation aux résidus énièmes, l'extension doit contenir
![]() , une racine énième primitive de l'unité (i.e.
, une racine énième primitive de l'unité (i.e. ![]() et
et
![]() ). Nous désignerons, conventionnellement
voire traditionnellement, un idéal premier par la lettre
). Nous désignerons, conventionnellement
voire traditionnellement, un idéal premier par la lettre ![]() (ou
(ou ![]() ), P majuscule (ou minuscule) en alphabet gothique,
en honneur à l'école algébrique allemande : en effet Kummer a introduit
ses 'nombres idéaux' en 1844 [Dahan], puis Dedekind a développé
la théorie des idéaux premiers.
Dedekind, dans le Supplément aux `` Vorselungen über Zahlentheorie ''
de Dirichlet, 1871, a introduit explicitement les notions de corps, d'anneau,
de module et d'idéal.
), P majuscule (ou minuscule) en alphabet gothique,
en honneur à l'école algébrique allemande : en effet Kummer a introduit
ses 'nombres idéaux' en 1844 [Dahan], puis Dedekind a développé
la théorie des idéaux premiers.
Dedekind, dans le Supplément aux `` Vorselungen über Zahlentheorie ''
de Dirichlet, 1871, a introduit explicitement les notions de corps, d'anneau,
de module et d'idéal.
Les idéaux premiers ![]() de
de ![]() qui ne divisent pas n vérifient
qui ne divisent pas n vérifient
![]() où
où ![]() est la norme
de l'idéal
est la norme
de l'idéal ![]() , égale au nombre de classes du plus grand ordre du corps
modulo
, égale au nombre de classes du plus grand ordre du corps
modulo ![]() , dit plus simplement,
, dit plus simplement, ![]() est le cardinal de
est le cardinal de ![]() lorsque
lorsque
![]() est un idéal de l'anneau
est un idéal de l'anneau ![]() des entiers du corps
des entiers du corps ![]() .
L'analogue du symbole de Legendre est défini par
.
L'analogue du symbole de Legendre est défini par
![]() . Tout comme pour le symbole de Jacobi, si
. Tout comme pour le symbole de Jacobi, si ![]() est
la décomposition de l'idéal principal (b) en idéaux premiers,
et si a et b sont des entiers algébriques étrangers, alors :
est
la décomposition de l'idéal principal (b) en idéaux premiers,
et si a et b sont des entiers algébriques étrangers, alors :
![]() .Si, avec ce symbole de résidu n-ième, on a
.Si, avec ce symbole de résidu n-ième, on a ![]() , alors
il existe un entier algébrique
, alors
il existe un entier algébrique ![]() tel que
tel que ![]() .
.
La loi de réciprocité pour n=4 dans le corps ![]() a
été établie par Gauss. Pour n=3 dans le
corps
a
été établie par Gauss. Pour n=3 dans le
corps ![]() , elle a été établie par Eisenstein :
Beweis des Reziprozitätgesetze für cübischen Reste, J. Math., 1844,
utilisant la formule
, elle a été établie par Eisenstein :
Beweis des Reziprozitätgesetze für cübischen Reste, J. Math., 1844,
utilisant la formule